题目大意：

Neighbor Grid

一个二维数组中任意位置的元素k周围（上下左右）有k个相邻的不为0的数的个数。
对二维数组的元素加一，能否构造出这样的二维数组。

思路：

贪心，直接将每个位置的值开到最大，例如对于4x4的矩阵：

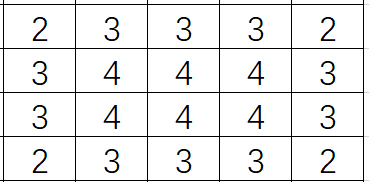
所以只需要判断相应的位置能否通过加一的操作达到相应位置的最大值。

AC Code:

#include<cstdio>
#include <iostream>
using namespace std;
int main()
{
    int t;
    cin >> t;
    while (t--)
    {
        int n, m, mp[309][309], flag = 0;
        cin >> n >> m;
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < m; j++)
            {
                cin >> mp[i][j];
                if (mp[i][j] > 4)
                    flag = 1;
                if (((i == 0 && j == 0) || (i == 0 && j == m - 1) || (i == n - 1 && j == 0) || (i == n - 1 && j == m - 1)) && mp[i][j] > 2)
                    flag = 1;
                else if (((i == 0 || j == 0 || i == n - 1 || j == m - 1)) && mp[i][j] > 3)
                    flag = 1;
            }
        }
        if (flag)
        {
            cout << "NO" << endl;
        }
        else
        {
            cout << "YES" << endl;
            for (int i = 0; i < n; i++)
            {
                for (int j = 0; j < m; j++)
                {
                    if ((i == 0 && j == 0) || (i == 0 && j == m - 1) || (i == n - 1 && j == 0) || (i == n - 1 && j == m - 1))
                        cout << 2 << " ";
                    else if (i == 0 || j == 0 || i == n - 1 || j == m - 1)
                        cout << 3 << " ";
                    else
                        cout << 4 << " ";
                }
                cout << endl;
            }
        }
    }
    return 0;
}